力扣221.最大正方形题解
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
示例 1:

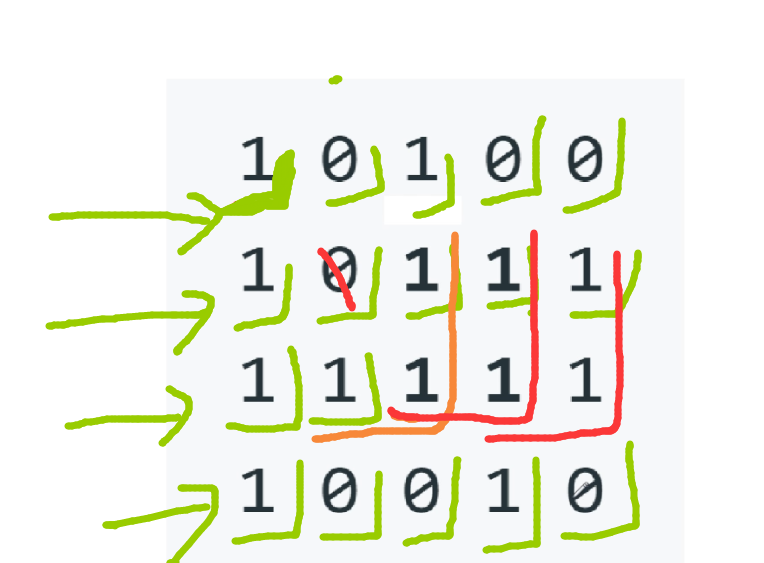
输入:matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]
输出:4
示例 2:

输入:matrix = [[“0”,”1”],[“1”,”0”]]
输出:1
示例 3:
输入:matrix = [[“0”]]
输出:0
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximal-square
这道题可以这样理解,逐个遍历,把每次遍历的地方当成该正方形的右下角,然后分别在该格子处向上,向左,向左上角试探,找寻满足正方形的格子,如果该格子在第一行或者第一列,那么就把最大值记为1或者0,把长度记下来平方即可求得面积
代码
1 | class Solution { |
结果