力扣133.克隆图题解
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public Listneighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
示例 2:
输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
示例 3:
****.**adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。
示例 4:
输入:adjList = [[2],[1]]
输出:[[2],[1]]
提示:
节点数不超过 100 。
每个节点值 Node.val 都是唯一的,1 <= Node.val <= 100。
无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
图是连通图,你可以从给定节点访问到所有节点。
解析:
让我们返回深拷贝,仔细看题目的话不难发现本题的要求是给我们一个图的入口,我们需要在入口对图进行一个遍历,我们在遍历的过程中要做两件事,第一就是把遇到节点的值给拷贝出来,拷贝到一个新的空间中去,第二件事就是把值拷贝完了之后还需要把这个点与点之间的关系给拷贝出来,在给定的代码里面就是要把neighbors这个关系拷贝出来,也放到新的空间中去
那么我们知道了本题的考察点就是遍历,那我们可以通过bfs和dfs来解题,但是无论是dfs还是bfs我们都需要去维护一个新老节点的关系,我们设原先的节点为old node,新的节点为new node,还需要一个map来维护这样的一个映射关系,因为本体的本质就是遍历,dfs和bfs的时空复杂度都是一样的(即O(n)),我用dfs来试着解题,
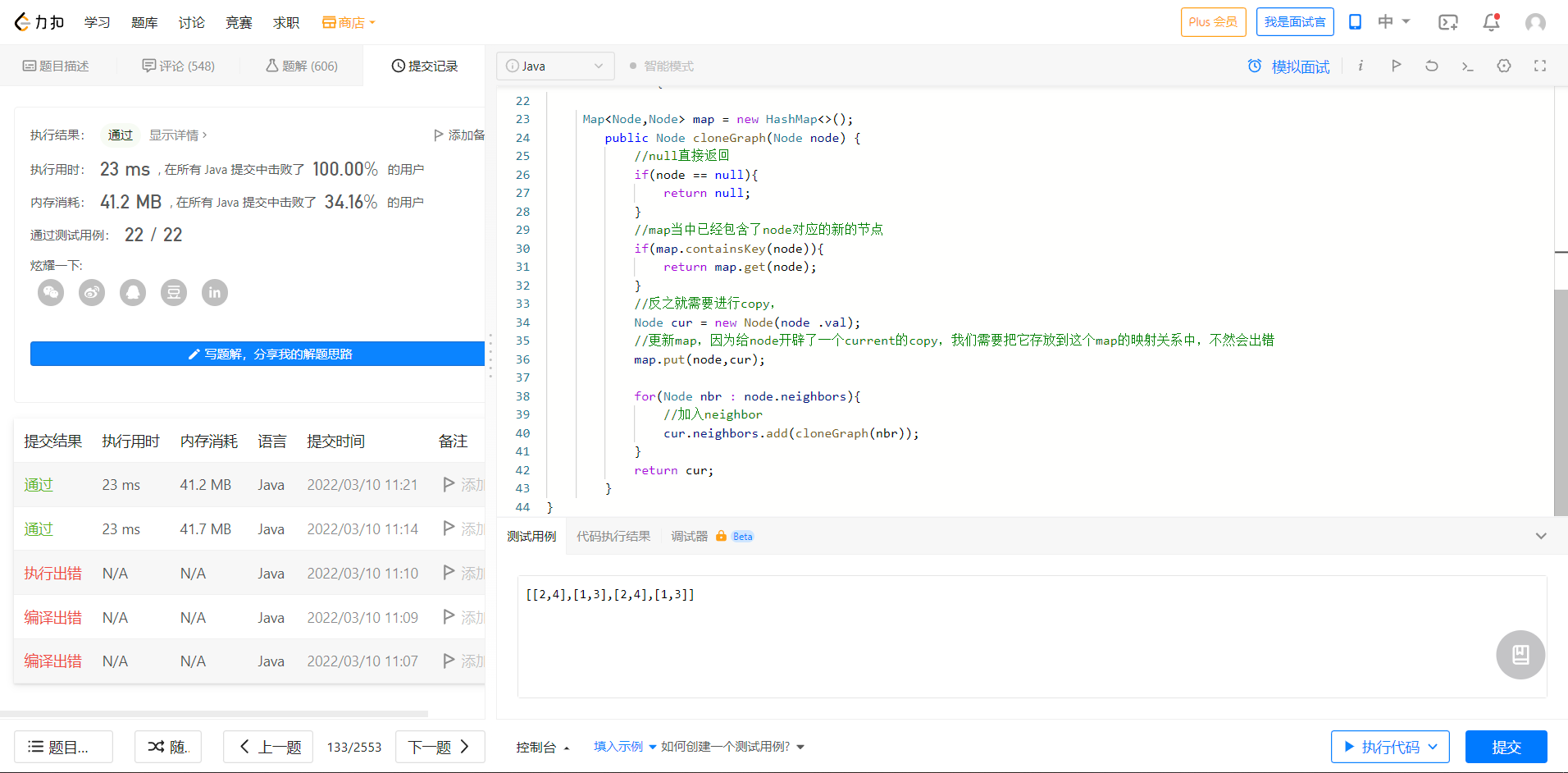
代码:
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
class Solution {
Map<Node,Node> map = new HashMap<>();
public Node cloneGraph(Node node) {
//null直接返回
if(node == null){
return null;
}
//map当中已经包含了node对应的新的节点
if(map.containsKey(node)){
return map.get(node);
}
//反之就需要进行copy,
Node cur = new Node(node .val);
//更新map,因为给node开辟了一个current的copy,我们需要把它存放到这个map的映射关系中,不然会出错
map.put(node,cur);
``
for(Node nbr : node.neighbors){
//加入neighbor
cur.neighbors.add(cloneGraph(nbr));
}
return cur;
}
}
运行截图: