力扣218. 天际线问题解析
城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示,其中三元组 buildings[i] = [lefti, righti, heighti] 表示:
lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
你可以假设所有的建筑都是完美的长方形,在高度为 0 的绝对平坦的表面上。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],…] ,并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[…[2 3], [4 5], [12 7], …]
示例 1:
输入:buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释:
图 A 显示输入的所有建筑物的位置和高度,
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
示例 2:
输入:buildings = [[0,2,3],[2,5,3]]
输出:[[0,3],[5,0]]
提示:
1 <= buildings.length <= 104
0 <= lefti < righti <= 231 - 1
1 <= heighti <= 231 - 1
buildings 按 lefti 非递减排序
解析:
这个题目的要求很明确,输入的是每个建筑物在坐标中的x和y的坐标,要求我们输出关键点,显而易见的关键点就是高层建筑的左上角部分,但是由于建筑物的阴影遮罩问题,关键点是位于相对于高层建筑物的底层建筑物的相对投影处,我们需要建立一个算法来进行这个问题的求解。
找到一个非常不错的题解视频,引用了一下这个ppt:https://www.bilibili.com/video/BV1yq4y1J73s?from=search&seid=18167085271206266066&spm_id_from=333.337.0.0
我们这里用到的是这里用到的是所谓的扫描线用法,因为每一个建筑物有两条边平行与y轴,我们可以设置建筑物的将建筑物的左顶点坐标的y取负值,(输入给了每个建筑物的具体坐标,那我们就可以通过这一特点进行这一技巧的使用),我们需要新建立一个堆,具体用法结合图片所示:
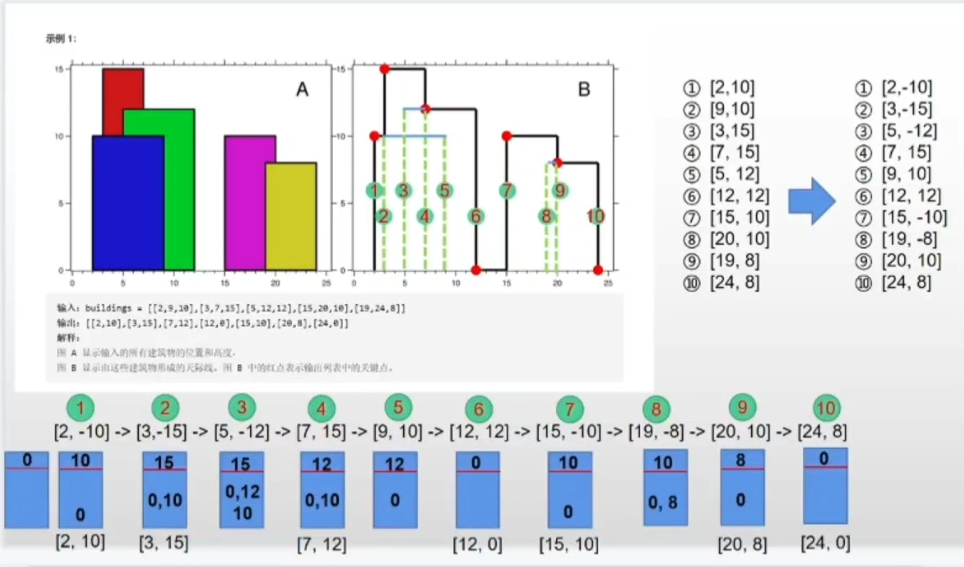
我们直接来看下面的1~10,规则就是遇到负数就把其换算成正数入堆,同时这个正数和堆中的其他正数进行比较大小,如果这个数字是最大的,就把x轴的坐标和该正数一起返回,如果不是最大的,进行下一个坐标的入堆/出堆,如果遇到了正数(即某一建筑物的右侧边缘),我们就需要对其在堆中的数据进行出堆,如果出堆的这个数字并不是堆中最大的数字,那么这个地方不是关键点,进行下一个坐标的入堆/出堆,如果是最大的,那么就把x轴的坐标和该正数一起返回。
简单总结边缘线算法那就是
从左自右扫描每一条边缘线,遇到左比阿奴原先koi入堆建筑物高度,遇到右边缘线就出堆建筑物高度
若堆内高度发生了变化,则表明遇到了天际线的关键点
关键点表示为当前边缘线的x的坐标和堆内最大值,即[x,queue.top()]
但是在代码实现逻辑上我们还需要注意一种情况
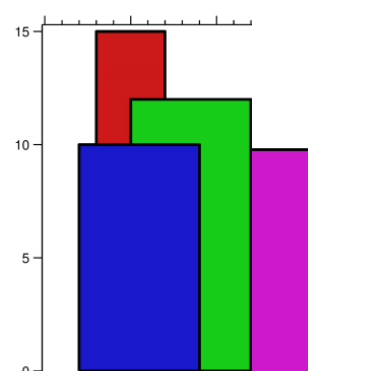
现在紫色建筑物和绿色建筑物投影链接在一起,我们入堆的时候就需要由低到高入堆,不然扫描到绿色建筑物就会弹出,导致x,0成为关键点
具体实现如下:
我使用的是大顶堆,并设置了第一个堆内元素,这样就能扫到第一个关键点,然后就行扫描比对删除就可以了,但是我们弹出堆的时候只能弹出对应的数值,而不是大顶堆只能弹出最大的那个数
代码:
class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
List<List<Integer>> points = new ArrayList<>();
//求出左上角和右上角坐标, 左上角坐标的 y 存负数
for (int[] b : buildings) {
points.add(Arrays.asList(b[0], -b[2]));
points.add(Arrays.asList(b[1], b[2]));
}
//将所有坐标排序
points.sort(
(O1, O2) -> {
int x1 = O1.get(0), y1 = O1.get(1);
int x2 = O2.get(0), y2 = O2.get(1);
//这个就是对特殊情况的处理,由小变大
if (x1 != x2) return x1 - x2;
else return y1 - y2;
});
//默认的优先队列是小顶堆,我们需要大顶堆(算是吧),每次需要得到队列中最大的元素
Queue<Integer> queue = new PriorityQueue<>((O1, O2) -> O2 - O1);
queue.offer(0);
int preMax = 0;
List<List<Integer>> res = new ArrayList<>();
for (List<Integer> p : points) {
int x = p.get(0), y = p.get(1);
//左上角坐标
if (y < 0) queue.offer(-y);
//右上角坐标
else queue.remove(y);
int curMax = queue.peek();
//最大值更新了, 将当前结果加入
if (curMax != preMax) {
res.add(Arrays.asList(x, curMax));
preMax = curMax;
}
}
return res;
}
}
截图: